Vector Databases – Part 3 – Vector Search
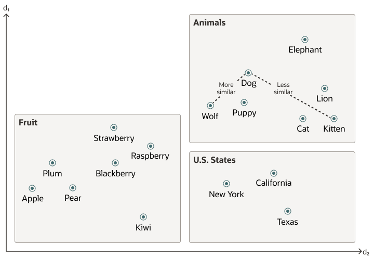
Searching semantic similarity in a data set is now equivalent to searching for nearest neighbors in a vector space instead of using traditional keyword searches using query predicates. The distance between “dog” and “wolf” in this vector space is shorter than the distance between “dog” and “kitten”. A “dog” is more similar to a “wolf” than it is to a “kitten”.
Vector data tends to be unevenly distributed and clustered into groups that are semantically related. Doing a similarity search based on a given query vector is equivalent to retrieving the K-nearest vectors to your query vector in your vector space.
Typically, you want to find an ordered list of vectors by ranking them, where the first row in the list is the closest or most similar vector to the query vector, the second row in the list is the second closest vector to the query vector, and so on. When doing a similarity search, the relative order of distances is what really matters rather than the actual distance.
Semantic search where the initial vector is the word “Puppy” and you want to identify the four closest words. Similarity searches tend to get data from one or more clusters depending on the value of the query vector, distance and the fetch size. Approximate searches using vector indexes can limit the searches to specific clusters, whereas exact searches visit vectors across all clusters.
Measuring distances in a vector space is the core of identifying the most relevant results for a given query vector. That process is very different from the well-known keyword filtering in the relational database world, which is very quick, simple and very very efficient. Vector distance functions involve more complicated computations.
There are several ways you can calculate distances to determine how similar, or dissimilar, two vectors are. Each distance metric is computed using different mathematical formulas. The time taken to calculate the distance between two vectors depends on many factors, including the distance metric used as well as the format of the vectors themselves, such as the number of vector dimensions and the vector dimension formats.
Generally, it’s best to match the distance metric you use to the one that was used to train the vector embedding model that generated the vectors. Common Distance metric functions include:
- Euclidean Distance
- Euclidean Distance Squared
- Cosine Similarity [most commonly used]
- Dot Product Similarity
- Manhattan Distance Hamming Similarity
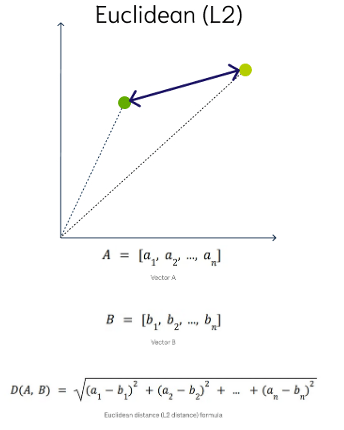
Euclidean Distance
This is a measure of the straight line distance between two points in the vector space. It ranges from 0 to infinity, where 0 represents identical vectors, and larger values represent increasingly dissimilar vectors. This is calculated using the Pythagorean theorem applied to the vector’s coordinates.
This metric is sensitive to both the vector’s size and it’s direction.
Euclidean Distance Squared
This is very similar to Euclidean Distance. When ordering is more important than the distance values themselves, the Squared Euclidean distance is very useful as it is faster to calculate than the Euclidean distance (avoiding the square-root calculation)
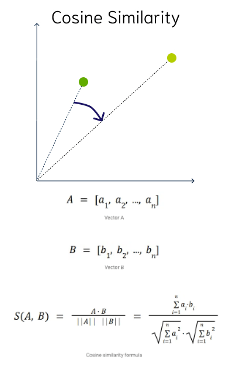
Cosine Similarity
This is the most commonly used distance measure. The cosine of the angle between two vectors – the larger the cosine, the closer the vectors. The smaller the angle, the bigger is its cosine. Cosine similarity measures the similarity in the direction or angle of the vectors, ignoring differences in their size (also called magnitude). The smaller the angle, the more similar are the two vectors. It ranges from -1 to 1, where 1 represents identical vectors, 0 represents orthogonal vectors, and -1 represents vectors that are diametrically opposed
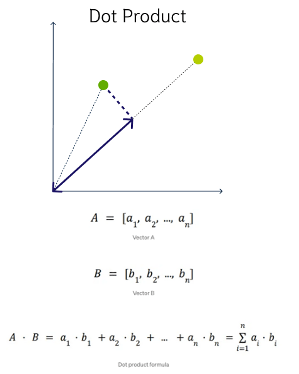
DOT Product Similarity
DOT product similarity of two vectors can be viewed as multiplying the size of each vector by the cosine of their angle. The larger the dot product, the closer the vectors. You project one vector on the other and multiply the resulting vector sizes. Larger DOT product values imply that the vectors are more similar, while smaller values imply that they are less similar. It ranges from -∞ to ∞, where a positive value represents vectors that point in the same direction, 0 represents orthogonal vectors, and a negative value represents vectors that point in opposite directions
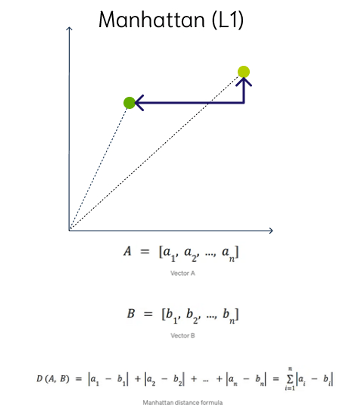
Manhattan Distance
This is calculated by summing the distance between the dimensions of the two vectors that you want to compare.
Imagine yourself in the streets of Manhattan trying to go from point A to point B. A straight line is not possible.
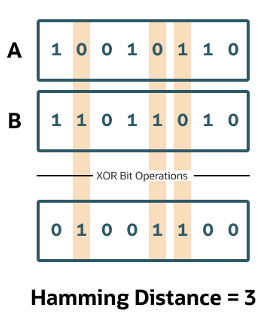
Hamming Similarity
This is the distance between two vectors represented by the number of dimensions where they differ. When using binary vectors, the Hamming distance between two vectors is the number of bits you must change to change one vector into the other. To compute the Hamming distance between two vectors, you need to compare the position of each bit in the sequence.
Check out my other posts in this series on Vector Databases.
Ora-lytics 